To Read My Papers on ArXiv, click here. Journal references are given there.
See My Publication on AU SciVal page here.
To see My Publication List on Loop, click here.
RECENT RESEARCH HIGHLIGHTS
A statistical mechanics perspective for protein folding from q -state Potts model [https://arxiv.org/abs/1709.04813 ].
The folding of a peptide chain into a three dimensional structure is a thermodynamically driven process such that the chain naturally evolves to form domains of similar amino acids. The formation of this domain occurs by curling the one dimensional amino acid sequence by moving similar amino acids proximity to each other. We model this formation of domains or ordering of amino acids using q-state Potts model and study the thermodynamic properties using a statistical mechanics approach. Converting the interacting amino acids into an effectively non-interacting model using a mean-field theory, we calculate the Helmholtz free energy (HFE). Then by investigating the HFE, we study the properties of protein folding transition qualitatively. We find that the protein folding phase transition is a strongly first order and the specific heat shows the experimental signatures of this phase transition. Further, we compare these mean-field results with exact transfer matrix results in one dimension and then large q expansion results in two dimensions.
For details see: https://arxiv.org/abs/1709.04813
The folding of a peptide chain into a three dimensional structure is a thermodynamically driven process such that the chain naturally evolves to form domains of similar amino acids. The formation of this domain occurs by curling the one dimensional amino acid sequence by moving similar amino acids proximity to each other. We model this formation of domains or ordering of amino acids using q-state Potts model and study the thermodynamic properties using a statistical mechanics approach. Converting the interacting amino acids into an effectively non-interacting model using a mean-field theory, we calculate the Helmholtz free energy (HFE). Then by investigating the HFE, we study the properties of protein folding transition qualitatively. We find that the protein folding phase transition is a strongly first order and the specific heat shows the experimental signatures of this phase transition. Further, we compare these mean-field results with exact transfer matrix results in one dimension and then large q expansion results in two dimensions.
For details see: https://arxiv.org/abs/1709.04813
Metal-Insulator-Superconductor transition of spin-3/2 atoms on optical lattices [Phys. Rev. A 97, 013632 (2018) ].
We use a slave-rotor approach within a mean-field theory to study the competition of metallic, Mott-insulating, and superconducting phases of spin-3/2 fermions subjected to a periodic optical lattice potential. In addition to the metallic, the Mott-insulating, and the superconducting phases that are associated with the gauge symmetry breaking of the spinon field, we identify a novel emerging superconducting phase that breaks both roton and spinon field gauge symmetries. This novel superconducting phase emerges as a result of the competition between spin-0 singlet and spin-2 quintet interaction channels naturally available for spin-3/2 systems. The two superconducting phases can be distinguished from each other by quasiparticle weight. We further discuss the properties of these phases for both two-dimensional square and three-dimensional cubic lattices at zero and finite temperatures.
For details see: Phys. Rev. A 97, 013632 (2018).
We use a slave-rotor approach within a mean-field theory to study the competition of metallic, Mott-insulating, and superconducting phases of spin-3/2 fermions subjected to a periodic optical lattice potential. In addition to the metallic, the Mott-insulating, and the superconducting phases that are associated with the gauge symmetry breaking of the spinon field, we identify a novel emerging superconducting phase that breaks both roton and spinon field gauge symmetries. This novel superconducting phase emerges as a result of the competition between spin-0 singlet and spin-2 quintet interaction channels naturally available for spin-3/2 systems. The two superconducting phases can be distinguished from each other by quasiparticle weight. We further discuss the properties of these phases for both two-dimensional square and three-dimensional cubic lattices at zero and finite temperatures.
For details see: Phys. Rev. A 97, 013632 (2018).
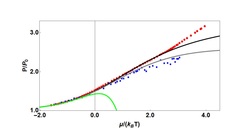
An effective series expansion to the equation of state of unitary Fermi gases [J. Phys. B: At. Mol. Opt. Phys. 49 225301 (2016)].
Using universal properties and a basic statistical mechanical approach, we propose a general equation of state for unitary Fermi gases. The universal equation of state is written as a series solution to a self consistent integral equation where the general solution is a linear combination of Fermi functions. First, by truncating our series solution to four terms with already known exact theoretical inputs at limiting cases, namely the first three virial coefficients and using the Bertsch parameter as a free parameter, we find a good agreement with experimental measurements in the entire temperature region in the normal state. This analytical equation of state agrees with experimental data up to the fugacity z = 18, which is a vast improvement over the other analytical equations of state available where the agreements is only up to z =7. Second, by truncating our series solution to four terms again using first four virial coefficients, we find the Bertsch parameter \xi =0.35, which is in good agreement with the direct experimental measurement of \xi =0.37. This second form of equation of state shows a good agreement with self-consistent T-matrix calculations in the normal phase.
For details see: J. Phys. B: At. Mol. Opt. Phys. 49 225301 2016.
Using universal properties and a basic statistical mechanical approach, we propose a general equation of state for unitary Fermi gases. The universal equation of state is written as a series solution to a self consistent integral equation where the general solution is a linear combination of Fermi functions. First, by truncating our series solution to four terms with already known exact theoretical inputs at limiting cases, namely the first three virial coefficients and using the Bertsch parameter as a free parameter, we find a good agreement with experimental measurements in the entire temperature region in the normal state. This analytical equation of state agrees with experimental data up to the fugacity z = 18, which is a vast improvement over the other analytical equations of state available where the agreements is only up to z =7. Second, by truncating our series solution to four terms again using first four virial coefficients, we find the Bertsch parameter \xi =0.35, which is in good agreement with the direct experimental measurement of \xi =0.37. This second form of equation of state shows a good agreement with self-consistent T-matrix calculations in the normal phase.
For details see: J. Phys. B: At. Mol. Opt. Phys. 49 225301 2016.
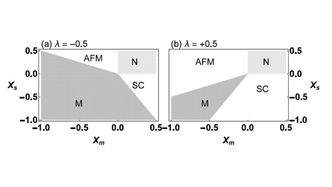
An effective mean-field theory for the coexistence of anti-ferromagnetism and superconductivity: Applications to Iron-based superconductors and cold Bose-Fermi atomic mixtures (Physics Letters A 380 (2016) 3421-3429).
We study an effective fermion model on a square lattice to investigate the cooperation and competition of superconductivity and anti-ferromagnetism. In addition to particle tunneling and on-site interaction, a bosonic excitation mediated attractive interaction is also included in the model. We assume that the attractive interaction is mediated by spin fluctuations and excitations of Bose-Einstein condensation (BEC) in electronic systems and Bose-Fermi mixtures on optical lattices, respectively. Using an effective mean-field theory to treat both superconductivity and anti-ferromagnetism at equal footing, we study the model within the Landau energy functional approach and a linearized theory. Within our approaches, we find possible co-existence of superconductivity and anti-ferromagnetism for both electronic and cold-atomic models. Our linearized theory shows while spin fluctuations favor d-wave superconductivity and BEC excitations favor s-wave superconductivity.
For details see: Physics Letters A380 (2016) 3421-3429.
We study an effective fermion model on a square lattice to investigate the cooperation and competition of superconductivity and anti-ferromagnetism. In addition to particle tunneling and on-site interaction, a bosonic excitation mediated attractive interaction is also included in the model. We assume that the attractive interaction is mediated by spin fluctuations and excitations of Bose-Einstein condensation (BEC) in electronic systems and Bose-Fermi mixtures on optical lattices, respectively. Using an effective mean-field theory to treat both superconductivity and anti-ferromagnetism at equal footing, we study the model within the Landau energy functional approach and a linearized theory. Within our approaches, we find possible co-existence of superconductivity and anti-ferromagnetism for both electronic and cold-atomic models. Our linearized theory shows while spin fluctuations favor d-wave superconductivity and BEC excitations favor s-wave superconductivity.
For details see: Physics Letters A380 (2016) 3421-3429.
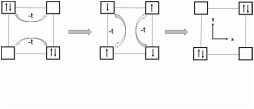
Phase diagram of strongly attractive p-orbital fermions on optical lattices (Physics Letters A 379 (2015) 2715–2722).
We examine a system of doubly degenerate p-orbital polarized fermions on a two-dimensional square lattice with a strong on-site interaction. We consider the system density at the half filling limit and tackle the strong attractive interaction using a perturbation theory. We treat the four-site square plaquette interaction term generated from the directional tunneling dependence of p-orbitals using the fourth order in perturbation theory. We map the strong coupling particle Hamiltonian into an effective spin-Hamiltonian and then use a variational mean field approach and a linear spin-wave theory to study the phase diagram. Further, we discuss the experimental signatures of these phases within the context of current cold-atom experimental techniques.
For details see: Physics Letters A 379 (2015) 2715–2722.
We examine a system of doubly degenerate p-orbital polarized fermions on a two-dimensional square lattice with a strong on-site interaction. We consider the system density at the half filling limit and tackle the strong attractive interaction using a perturbation theory. We treat the four-site square plaquette interaction term generated from the directional tunneling dependence of p-orbitals using the fourth order in perturbation theory. We map the strong coupling particle Hamiltonian into an effective spin-Hamiltonian and then use a variational mean field approach and a linear spin-wave theory to study the phase diagram. Further, we discuss the experimental signatures of these phases within the context of current cold-atom experimental techniques.
For details see: Physics Letters A 379 (2015) 2715–2722.
Polarization-induced phase separation and re-entrant transition of two-component fermions in a one-dimensional lattice (Phys. Rev. A 91, 053627, 2015)
By investigating the compressibility of one-dimensional lattice fermions at various filling factors, we study the phase separation and re-entrant transition within the framework of the Bethe ansatz method. We model the system using the repulsive Hubbard model and calculate compressibility as a function of polarization for arbitrary values of chemical potential, temperature, and interaction strength. For filling factors 0<n<1, compressibility is a nonmonotonic function of polarization at all thermodynamic parameters. The compressibility reveals a phase transition into a phase-separated state for both low and intermediate temperatures at intermediate interactions as one increases the polarization. For certain filling factors, we find the re-entrant transition into the mixed phase at a higher polarization.
For details see: Physical Review A Phys. Rev. A 91, 053627 (2015).
By investigating the compressibility of one-dimensional lattice fermions at various filling factors, we study the phase separation and re-entrant transition within the framework of the Bethe ansatz method. We model the system using the repulsive Hubbard model and calculate compressibility as a function of polarization for arbitrary values of chemical potential, temperature, and interaction strength. For filling factors 0<n<1, compressibility is a nonmonotonic function of polarization at all thermodynamic parameters. The compressibility reveals a phase transition into a phase-separated state for both low and intermediate temperatures at intermediate interactions as one increases the polarization. For certain filling factors, we find the re-entrant transition into the mixed phase at a higher polarization.
For details see: Physical Review A Phys. Rev. A 91, 053627 (2015).
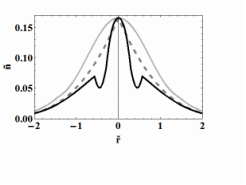
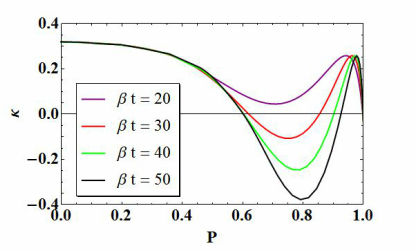
Evidence for the breakdown of momentum independent many-body t-matrix approximation in the normal phase of Bosons (Front. Phys. 2, 78, 2014)
We revisit the momentum independent many-body t-matrix approach for boson systems developed by Shi and Griffin and Bijlsma and Stoof. Despite its popularity, simplicity, and expected advantage of being its applicability to both normal and superfluid phases, we find that the theory breaks down in the normal phase of bosons. We conjecture that this failure is due to neglecting of momentum dependence on the t-matrix.
For details see: Frontiers of Physics Front. Phys. 2:78. doi: 10.3389/fphy.2014.00078.
We revisit the momentum independent many-body t-matrix approach for boson systems developed by Shi and Griffin and Bijlsma and Stoof. Despite its popularity, simplicity, and expected advantage of being its applicability to both normal and superfluid phases, we find that the theory breaks down in the normal phase of bosons. We conjecture that this failure is due to neglecting of momentum dependence on the t-matrix.
For details see: Frontiers of Physics Front. Phys. 2:78. doi: 10.3389/fphy.2014.00078.
